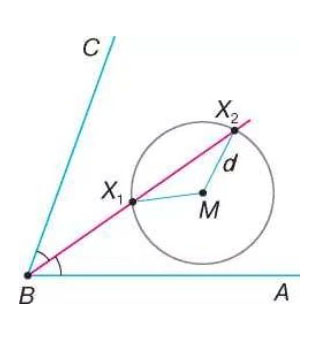
Геометричним місцем точок називається сукупність точок, які мають властивості, належні тільки їм. Якщо задача зводиться до визначення точки, то можна відкинути одну з умов, яку ця точка повинна задовольняти; тоді шукана точка зможе набути нескінченну множину послідовних положень, і всі ці положення становитимуть геометричне місце точок, які мають усі потрібні властивості, крім відкинутої. Форма цього геометричного місця найчастіше буває відомою наперед; в противному разі її треба визначити допоміжними умовами. Потім, узявши відкинуту умову і відкинувши будь-яку іншу умову задачі, ми знову побачимо, що шукана точка може набути нескінченну множину нових положень, що утворюють нове геометричне місце. Визначимо форму цього нового геометричного місця, якщо вона нам невідома. Тоді шукана точка повинна лежати і на першому і на другому геометричному місці, а тому визначається їх перетином. Іноді для визначення точки досить побудувати одне геометричне місце, бо друге дано в умові задачі. Якщо ж шукана точка підпорядкована таким умовам, що вони всі в сукупності визначають тільки одне геометричне місце точок, то задача стає неозначеною.

Залежно від виду перетворення при розв'язуванні задач на побудову використовуємо метод симетрії, метод повороту, метод паралельного перенесення та метод подібності. Ідея застосування методів перетворення до розв'язування задач на побудову така: якщо властивості шуканих елементів фігури, яку потрібно побудувати, неможливо знайти при безпосередньому вивченні малюнка-ескіза, то перетворюють геометрично або всю фігуру, зображену на малюнку-ескізі, або її елементи. Після цього легше виявити властивості шуканих елементів фігури і знайти стосіб побудови.

Суть методу полягає в тому, що, проводячи аналіз задачі на побудову, положення на площині шуканого елемента знаходимо за допомогою алгебри. Припустивши, що задачу розв'язано, виділяємо на малюнку-ескізі шуканий елемент, до визначення якого зводиться розв'язування задачі. На підставі умови задачі і геометричних теорем складаємо рівняння, розв'язуючи яке знаходимо для шуканого елемента алгебраїчний вираз. Побудувавши його за допомогою креслярських інструментів, знаходимо положення шуканого елемента, а отже, і спосіб розв'язування задачі.