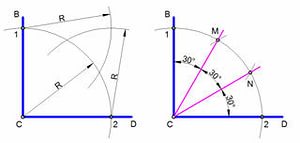
Математики Стародавнього світу, як правило, багато задач розв'язували геометричним способом, використовуючи різні спеціальні прилади. Наприклад, вони могли за допомогою циркуля і лінійки порівняно легко побудувати суму і різницю двох відрізків, поділити кут навпіл, помножити відрізок на звичайний дріб. Використовуючи ці побудови можна було геометрично отримувати розв'язки лінійних і деяких квадратних рівнянь. 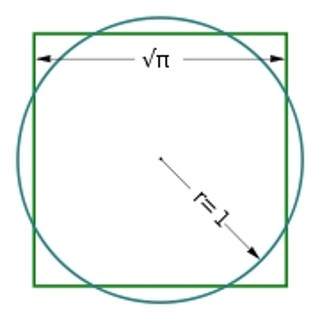Але на той час були сформульовані задачі, які неможливо розв'язати за допомогою циркуля і лінійки.

Згідно умови задачі, треба розв'язати рівняння х3 = 2∙а3, тобто треба побудувати добуток відрізка на ірраціональне число, рівне кубічному кореню з двійки. Вже доведено у першій половині ХІХ століття, що за допомогою циркуля і лінійки, без застосування інших допоміжних приладів, не можна геометрично побудувати відрізок, який би дорівнював кубічному кореню з двійки.

Для прямого кута, це зробити можна, якщо на обох сторонах кута побутувати правильні(рівносторонні) трикутники, зі спільною вершиною, яка співпадає з вершиною прямого кута. Згодом вияснили, що ця задача є нерозв'язною для циркуля та лінійки. Це строго довів в 1837 році П. Ванцель.

Було дуже багато спроб розв'язати задачу про квадратуру круга за допомогою циркуля та лінійки. Але спроби давньогрецьких вчених розв'язати задачу про квадратуру круга шляхом проведення прямих та кіл так і не мали успіху. Воно й зрозуміло чому. Справа в тім, що задача про квадратуру круга, так як і задачі про подвоєння куба і трисекції кута, являється також нерозв'язною за допомогою циркуля та лінійки. Німецькому математику Ф. Ліндеману в 1882 р. вдалося, накінець, цілком строго довести, що задача про квадратуру круга нерозв'язна за допомогою циркуля та лінійки і усі старання що-небудь зробити в цьому напрямі вказаними засобами є просто безглудими.